A number of years ago, at my first job out of college, I was working for a company that found itself in the swell of the then-nascent cloud computing wave. The work that my team did was mainly write proofs-of-concept for new products that would then be scaled in collaboration with a broader, global engineering team. There was one “concept” that I had in mind, though, that, due to various competing team priorities, I never got to work on and “prove.” It was in relation to applying Reed-Solomon encoding to the problem of distributed file storage, for some intriguing “mesh network”-like benefits. Unfortunately, before an opportunity to work on it could materialize, I had moved on to a different job in a different industry. As far as my dalliance with cloud computing went, this was the project that got away, and in idle moments over the years I often remembered it wistfully and wondered if anyone had tried anything like it.
Fast forward a decade and scrub past a worldwide pandemic to a couple of months ago, when I heard about a popular peer-to-peer filesystem and some of the challenges it is attempting to overcome. One of these challenges is high availability — how do you ensure that a user’s file is always available for them to download when they need it? Another is latency — how do you ensure fast downloads?
This immediately reminded me of the aforementioned concept, as I felt it represented a particularly elegant solution to these problems. I did a quick Google search and learned that apparently, nowadays, “erasure coding is standard practice” among cloud storage providers. I even came across this article on the subject that appears very similar to what I had in mind. Yet, it did not appear that the technique was as widely understood and widely applied as it could be, and in particular, does not appear to have been applied in a peer-to-peer setting. I felt this could be a good occasion to raise more awareness of the technologies it touches and the power and flexibility they lend. Since I’ve also lately been working on an initiative to address the economic problems of open source innovation, I felt I could kill two birds, as the terrible saying goes, by taking this on now, and so I decided to write the long-overdue proof-of-concept for wide consumption. So here goes — indulge me as I tell you about Jewel.
This is a story about technology, about people, and about value. It’s about all of these things at once, and although some fancy math is part of the story, I would say that it is only incidental to the broader points I’d like to make here, so honestly, feel free to skim the technical portions and read sections in any order you like — it will not take away from the essence, and I’ve even included a table of contents here for you to plan your approach. Indeed, I’m not sure how much of the technical aspects in this post (if any of it) will even be novel. By the end of this post, I hope you’ll walk away with an armchair appreciation of some neat math and how it could be applied in engineering, and side by side with that, gain some insight into the creation of value in the world and some food for thought on how we might do it more effectively.
Now, let’s roll up our sleeves and attend to the problem at hand!
The Problem
The essential problem a peer-to-peer filesystem needs to solve is this:
How can we securely store your data so that you can access it from anywhere at any time while minimizing the amount of storage used as well as the time taken to retrieve it?
Note that, for now, we are considering the specific problem of private file hosting rather than file sharing — you want to store your files “in the cloud” but, perhaps, don’t want to use one of the mainstream client and server style cloud storage providers such as Google Drive or Dropbox. Instead, you want to use a peer-to-peer network like Filecoin as your small way of sticking it to The Man and investing in decentralized infrastructure (incidentally, Filecoin was the impetus for this post).
There are many possible solutions, and we’ll go over some of them in order from simple to sophisticated, while discussing the benefits and drawbacks of each approach. Finally, we’ll get to the main solution that we are interested in in this post, “jewels,” implemented using Reed-Solomon encoding.
Solution A: Naive duplication
Store N copies of the file, each on a different peer (i.e. using N peers). Then, as long as at least one peer is available, you can get your file.
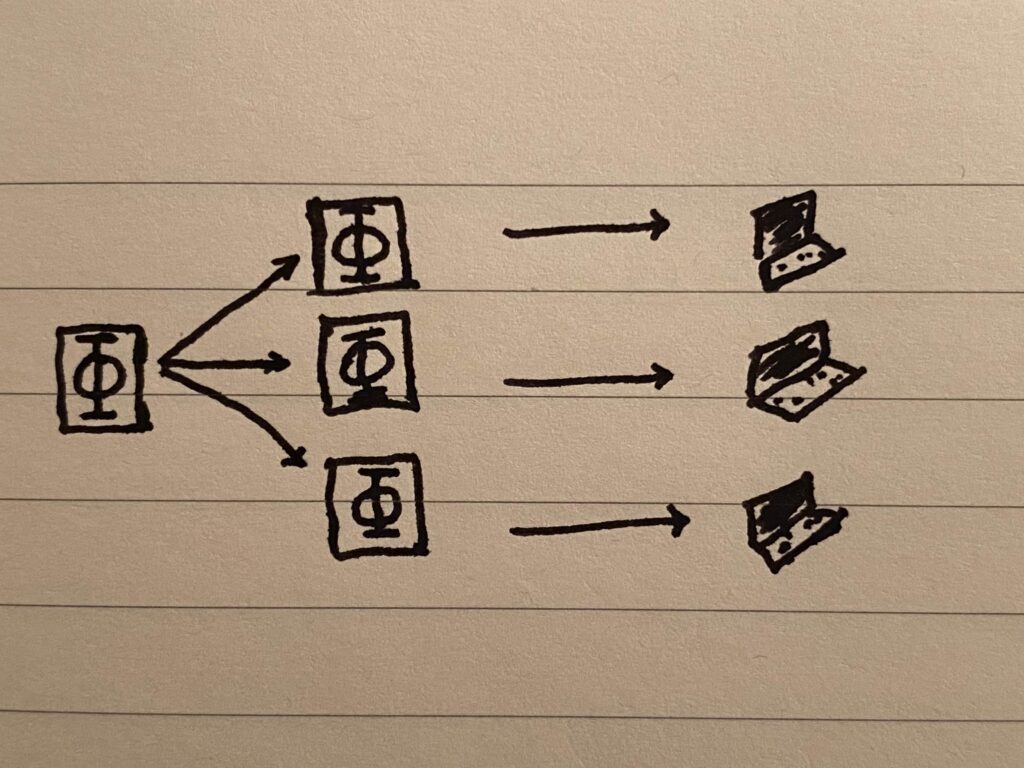
The way to make this solution more reliable is to increase N, and in this way we can get arbitrarily close to 100% availability. The cost is high redundancy (extra space used). We are only interested in the file itself, and a single copy suffices, yet, there are all these other copies just sitting around taking up space to shore up for the worst-case scenario. For this solution, the redundancy factor (let’s call it D) always equals the number of peers N used for storage.
Solution B: Sharding
Divide the file into K evenly-sized pieces or “shards” and store them, as before, across N peers. Individual peers may have more than one shard, but not necessarily the entire file. As a result, with this scheme, we’d need a certain minimum number of peers M to be online in order to get our data.
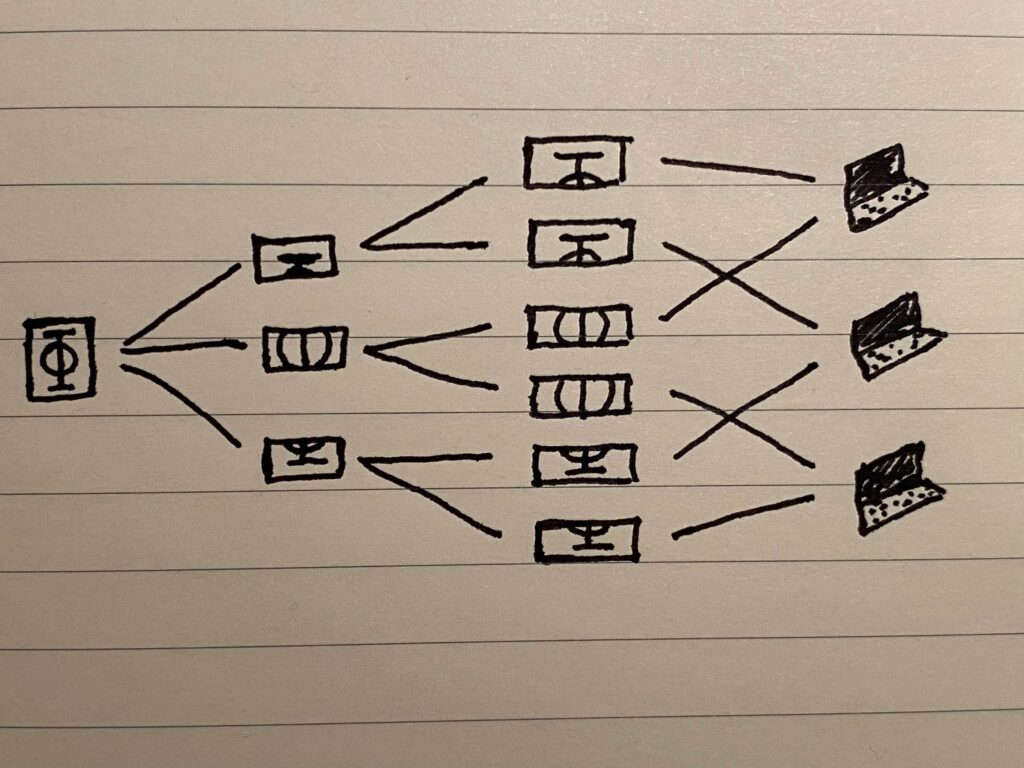
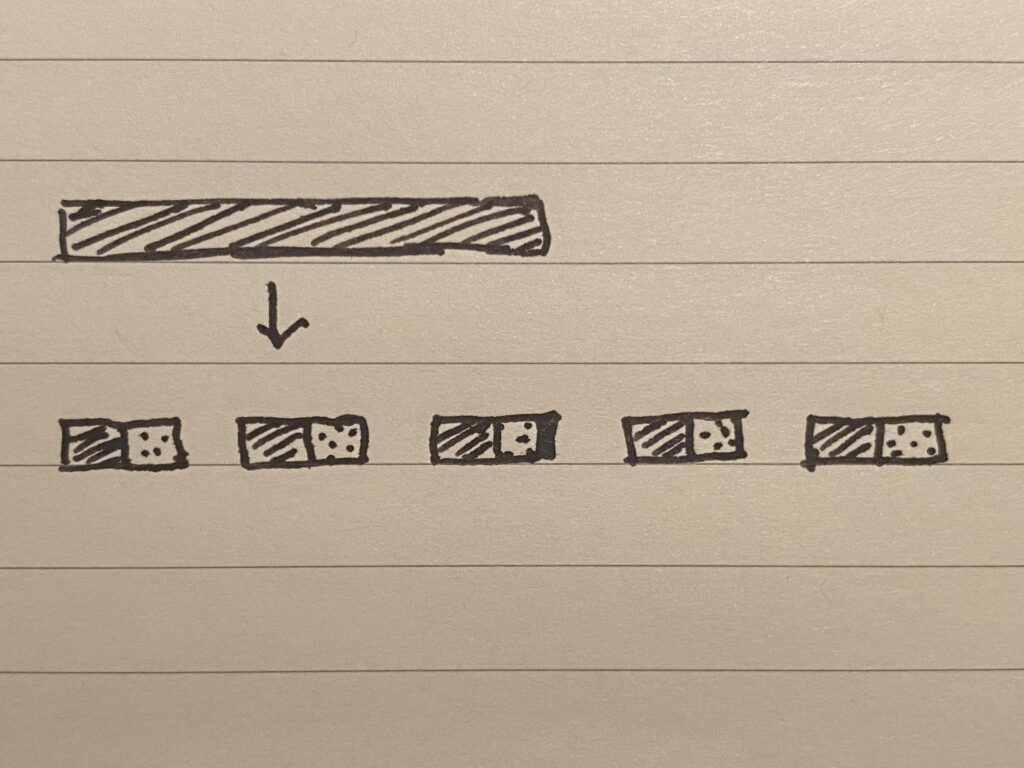
As an example, say we’d like to store a file across 3 peers, so that N=3. In solution A, this means that D=3 as well, i.e. we are storing 3x as much data as the size of the file.
For solution B, if we divide the file into 3 shards (call them 1, 2 and 3) and then stripe them across the 3 peers as [1,2,3], [1,2,3], [1,2,3], then this is identical to solution A. But we could also stripe the shards as [1,2], [1,3], [2,3] (as in the figure above), and in this case, D=2 (since we store two copies of every shard), and we need at least 2 peers to be online in order to get our file.
As this example illustrates, the main value of this solution is decoupling. It decouples the number of peers used for storage (N), the redundancy (D), and the minimum number of online peers needed (M), giving us the flexibility to tune these to our liking, or even, possibly, learn or dynamically tune the values in response to network health. In particular, this reduces to solution A in the boundary case where we store the full set of shards on each peer, as we saw.
By virtue of this decoupling, this solution opens up new possibilities, as exemplified by the remaining solutions.
Solution C: Sharding with parity
Same as solution B, but in addition to the M shards, we also create an extra “parity” shard which is the XOR of all of the M shards. This is done to take advantage of the convenient property of the XOR operation that it is “invertible” in the following way:
If a XOR b is c, then
a XOR c is b and
b XOR c is a
In other words, if one of the operands in the original XOR operation is missing, XOR’ing the remaining operands with the result of the original operation yields the missing operand.
In the case of our shards, this means that if any shard goes missing, we can reconstruct it by XOR’ing all of the remaining shards together with the parity shard.
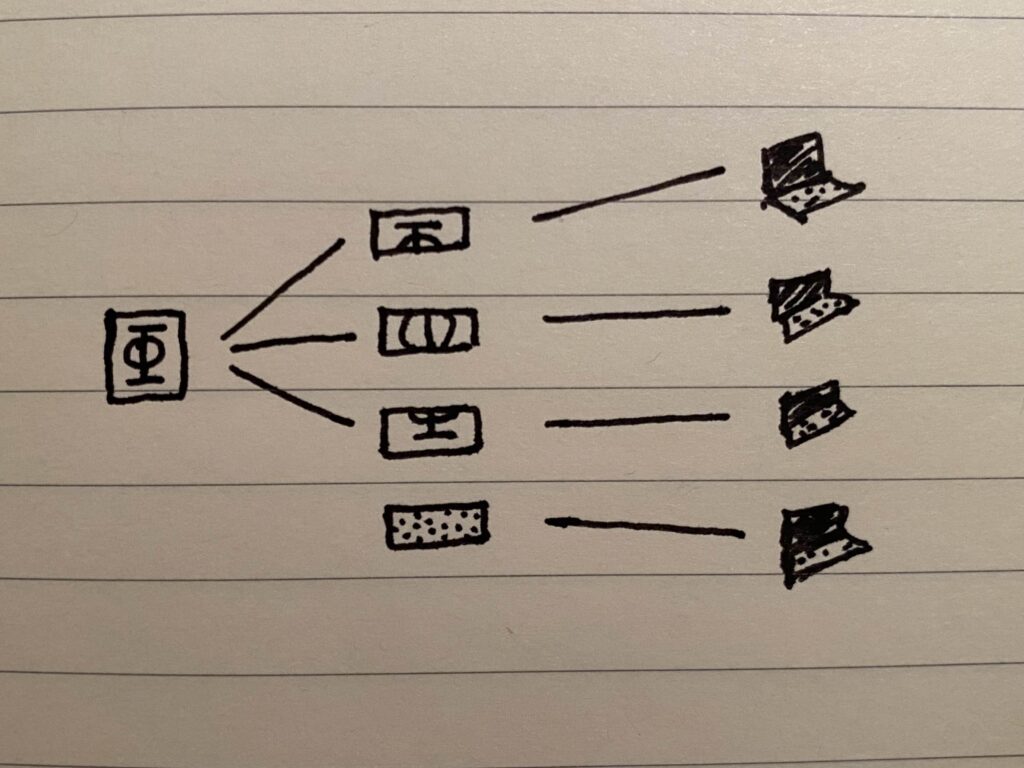
Using a parity shard in our distributed filesystem in this way is similar to one of the options used by RAID arrays for conventional hard drive storage, where one among many identically-sized disks in the array is designated as the parity disk. The purpose of this parity disk is to be able to reconstruct corrupted data on any of the other disks, by employing the XOR operation in this way.
This solution improves on B since, ordinarily, if we wanted extra redundancy, we’d need to duplicate all shards at least one extra time, otherwise any shards that have fewer copies than other shards would be “weak links” in the system. The parity approach allows us to create a single extra shard that gives us extra redundancy in any shard. We’ll refer to this property as the ability to add differential redundancy.
The problem is, we can only afford to lose one shard — either one of the original K shards, or the parity shard. As we can only add one shard’s worth of differential redundancy, if more than one distinct shard is unavailable, then this solution cannot recover.
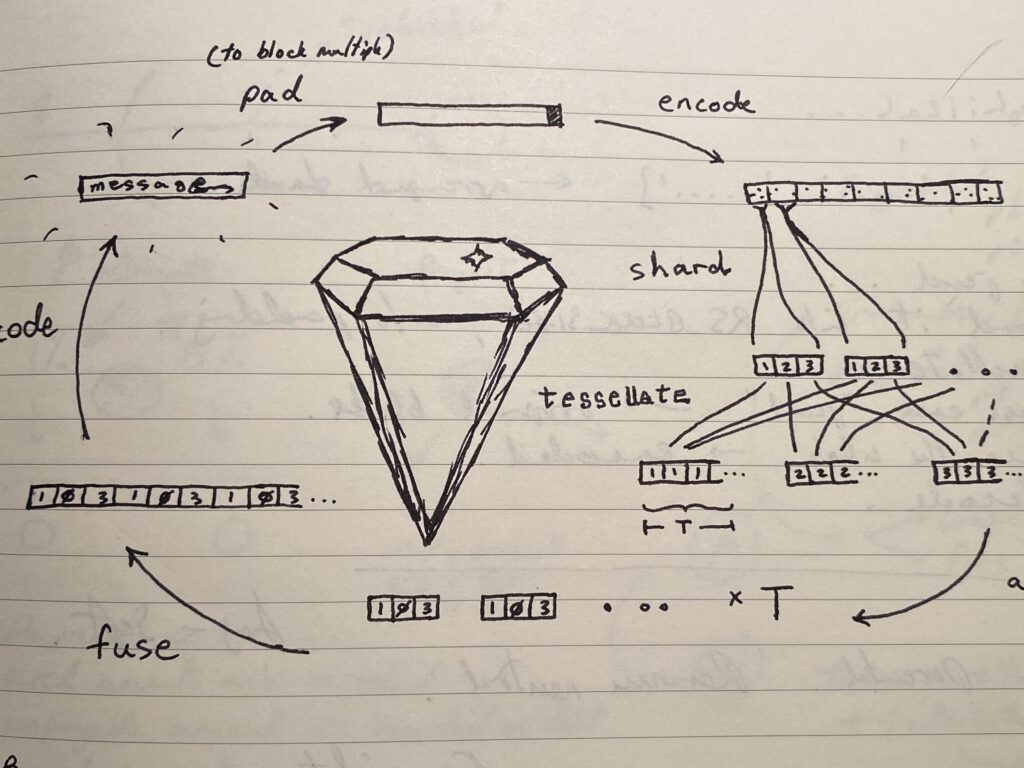
Solution D: “Jewels”
Once again, similar to Solution B, but here, we first encode the data using Reed-Solomon encoding and then store the resulting encoded data (rather than the original data) in specially constructed shards called “jewels.” But in order to understand this solution, we first need to understand a bit about Reed-Solomon codes.
Reed-Solomon is an error correcting code. Among other things, it is the encoding used in storing data on CDs, which is why they can still work even after being badly scratched — it’s not that the scratches don’t always destroy data, but that the encoding is able to recover the original data even though some of it is lost. The general idea of Reed-Solomon is that for any N numbers, there is a unique polynomial of N coefficients that takes on those values at the positions 1,2,3, …, N (this is called the “Lagrange Interpolation Theorem”). Once we determine this polynomial, we can compute any number of extra values on this curve and store those as “recovery” numbers. If any of the original numbers are lost, as long as you still have at least N numbers, you can compute the unique polynomial and then get the original values at positions 1 through N back. There are some theoretical nuances such as the use of a Galois Field (i.e. modular arithmetic) instead of the usual set of integers, but this is the general idea. In this way, Reed Solomon decoding recovers the larger pattern (the polynomial), of which your original data is contrived to be a part. This video is a good starting point for the ideas involved, if you’d like to learn more:
One other thing to know is that, for practical reasons, Reed-Solomon codes encode data in blocks of a certain size, for instance, 255 bytes. These blocks are typically much smaller than the files we wish to store which may be on the order of megabytes or gigabytes, so we can’t just encode an entire file directly. Instead, data to be encoded is typically “chunked,” then encoded independently to form the (e.g. 255 byte) blocks, and then concatenated to form the complete encoded file. Libraries implementing Reed-Solomon codes typically allow you to specify the level of redundancy you’d like on a per-block basis. For instance, you might configure it to use 200 bytes of your file followed by 55 bytes of recovery data in each block — this configuration is notated RS(255,200). This would mean that as long as there are at least 200 bytes intact at decoding time (for instance, in the example of a CD, if at least 200 of the 255 bytes are readable from the disc — and it doesn’t matter which ones), then it will be possible to reconstruct the polynomial and consequently the data. This will be important to know in piecing this solution together.
Now, here is the final piece of the puzzle. If there are, say, 10 peers to work with, then naively, the best we might do is divide the encoded file into 10 shards and store one on each peer. With no peer holding more than one shard, we may feel secure that if any of them goes down, it won’t be the end of the world. We might feel, too, that since we’ve baked enough redundancy into the encoding (for RS(255,200), that’s about 20% redundancy), that we should be pretty secure if a couple of these peers became unavailable. The problem is, since each block contains unique data, we can’t afford to lose even one block, let alone dozens or scores of them when a peer goes down, so this doesn’t work at all!
To solve this and complete the solution, instead of naively dividing the full encoded file into shards (which effectively means the shards are made up of naively concatenated 255-byte blocks), we instead shard each block, and then assemble the final shards (“jewels”) that will be stored on peers by concatenating all of the first “block” shards to form the first jewel, the second block shards to form the second jewel, and so on. As a result, every jewel has a piece of every block, and if some jewels go missing, we will always have pieces of all blocks left in the remaining jewels. By constructing the “jewels” this way, we ensure that every jewel equally reflects the overall pattern and can be used to reconstruct it (hence the name “jewel,” referencing Indra’s Net). Now we can afford to lose proportionally as many jewels as the proportion of recovery data we baked into each block, and just like the bytes in individual blocks, it doesn’t matter which of those jewels go missing, as long as there are enough (distinct) ones left.
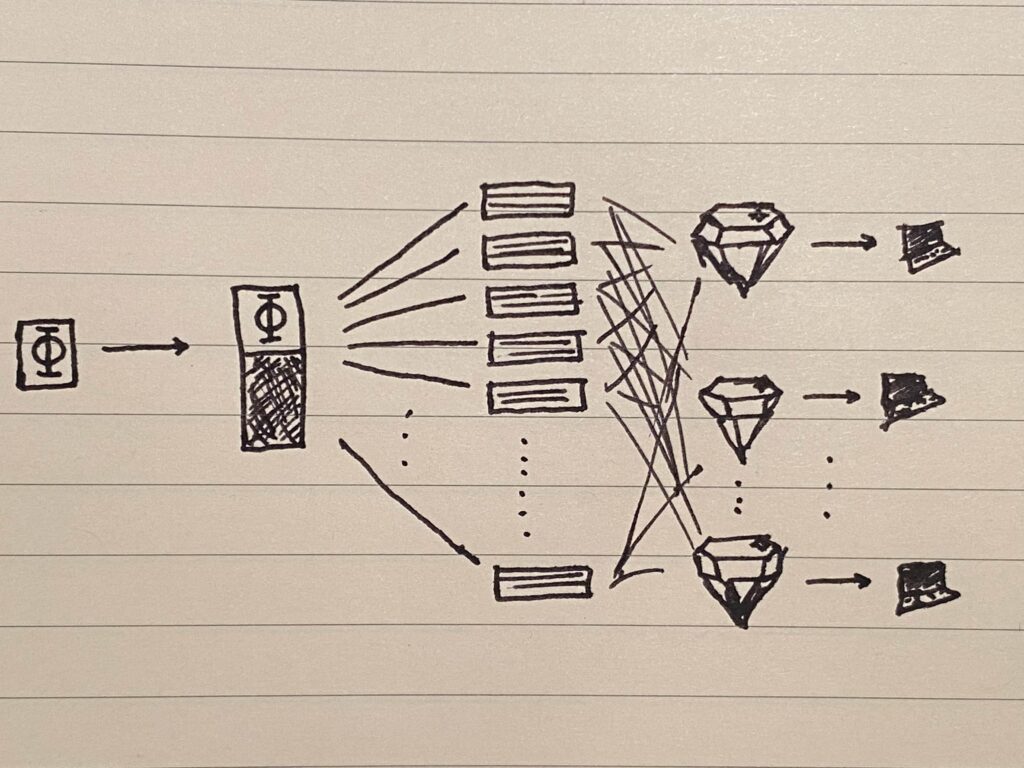
Incidentally, the operation of constructing jewels from Reed-Solomon blocks, and from reconstructing blocks again from jewels, turns out to be a simple matrix transpose operation, for which there are efficient implementations in linear algebra libraries like NumPy.
The key thing about this solution is that the jewels are all equivalent to one another for the purposes of recovering our data (more precisely, any subset of jewels is equivalent to any other of the same size), giving us maximum flexibility in tuning and balancing redundancy with availability. For instance, when sharding with parity, we can only afford to lose up to one shard, whereas with jewels, we can configure this differential redundancy to be any number we like. As another comparison, when sharding with 3x redundancy so that each shard is duplicated three times, if we have 5 shards for each file, then we have 15 shards total including copies. We could lose up to 10 shards if the ones that remain happen to all be distinct, but in the worst case, losing only three shards could be our undoing if the missing ones happen to all be copies of the same shard. With jewels, for the same redundancy (storing 3x the amount of data), we could always afford to lose up to 10 jewels!
The Prototype
I hope I’ve convinced you that jewels are a robust solution that offer a lot of flexibility in meeting changing storage needs. You can play with this or any other of these solutions in the proof-of-concept application here, where the README contains all the setup instructions you’ll need:
Now it’s important to remember that this isn’t a production-ready filesystem — it’s only a model of one; a simple prototyping environment where it would be easy to try out new ideas and new technologies before implementing it on a large scale in a production system. There are many design ideas implemented by the prototype, and many others that could be prototyped, and the barrier to entry is much lower than it might be in a production-scale filesystem, making it useful as a proving ground for trying things out and validating hypotheses.
For instance, one interesting design idea Jewel implements is to employ a “block” abstraction (unrelated to the Reed-Solomon blocks we have been talking about so far) to unify the filesystem’s representation of data. Rather than store files and shards, Jewel’s filesystem abstraction stores only “blocks.” Any data, whether compressed or not, encrypted or not, whole or partial, is considered a “block” in this sense, and is essentially the only concept the filesystem itself knows about — it is similar to Git’s concept of “blobs.” Another concept yet to be implemented is to organize the filesystem on strict hierarchy levels where the lowest level only knows about blocks and “fragments” (contiguous pieces of a block), while higher levels are aware of the nuances of particular storage schemes used, such as jewels or sharding or parity or anything else. There are still more concepts waiting to be implemented, such as employing compression and encryption at different levels to reduce cost and ensure privacy, and abstracting the storage scheme employed so that the means of storage is “virtual,” giving peers maximum flexibility in fulfilling the storage contract in whatever way is most convenient for them.
There may be many more interesting ideas you might think of that could be prototyped and proven using this application. Implementing it in Jewel is not a substitute for a production implementation in your platform of interest, but it could be a useful precursor to one.
An Opulent Vision
Aside from the specific concept illustrated by Jewel, it was my hope that you might see in it a glimmer of a possible future, a foreshadowing of the possibilities for the organic creation and recognition of value in the world, and for how decentralized infrastructure could help with that.
Let’s start with the personal story of Jewel itself. When I decided to work on it, I reached out to friends who I thought would be interested in working on it with me. The sad reality is that our existing economic machinery keeps all of us very busy and ensures that we have 0% availability 😉. Nevertheless, some friends were intrigued and offered useful suggestions and pointers for the implementation, and a few even helped debug some thorny issues. Even though few could spare the time, this effort was still enough to bring us together in a small and wholesome way. Now just imagine if we could be fairly compensated for doing this kind of fun, interesting, and valuable work out in the open, the same way as we are compensated when we do our work behind closed corporate doors. What might the world look like then? Would deep human connections be so elusive as they are today?
This is the problem Attribution Based Economics aims to solve. In one sentence, ABE is a movement (not a startup!) and economic model that allows you to work on whatever you like with whomever you like, and be fairly — financially — recognized for value contributed. It is an alternative to corporate-guided, ownership-oriented (e.g. requiring patents and copyright for their operation) value creation. You can learn a little more about it from my talk at EmacsConf:
Now, to bring this idea back to the specific problem we are focused on here: what could peer-to-peer networks (not just the human kind) look like in an ABE world?
Well, yesterday, such networks, like Napster, allowed us to share files with anyone in the world. Today, networks like Filecoin can host files just for you. We don’t need to share files with others so much anymore because we rely on centralized streaming services like Netflix and Spotify to host data that is of broad interest (such as movies and music). But although this arrangement is a hard-won and in some respects reasonable compromise when cast against the uncertainty and tumult of recent decades, it is far from ideal as a solution that serves the interests of the common good or even of the concerned parties. For starters, many artists don’t feel as though they receive a fair share of revenues earned by such streaming platforms. On the other hand, the often-maligned middlepersons provide value too and should be fairly recognized even if they aren’t content creators (though the need for such go-betweens should of course be minimized in service of efficiency and consequently cost). Finally, are consumers paying enough to begin with, when market forces are poorly defined for such content, and thus arguably tend to undervalue them? (These questions barely scratch the surface, and, for instance, there are many deep reasons why consumers are rightfully unwilling to pay more for such content today.) Who gets to decide what’s fair?
Additionally, as consumers we have to sign up for several such platforms in order to get access to more content, and even then, the many layers of copyright and legal red tape in which the actual content is ensnared ensures that we must search across these platforms for what we want, and waste precious time, not to mention be badgered by ads all along the way! Instead, we resign ourselves to watching what is available on the platform we signed up for, rather than the content we actually want, subtly yet firmly guided by the arbitrary weavings of red tape behind the scenes, whose warp and weft have nothing at all to do with the content we care about. Who gets to decide what you watch?
Instead, wouldn’t it be better if we could just have access to all content, all the time, in such a way that artists and creators are fairly compensated while minimizing logistical overhead?
A peer-to-peer storage system powered by ABE could achieve precisely this (I wonder if anyone has tried reconciling a differential redundancy solution like jewels with the needs of streaming?). In fact, it would contain not only the finished creative products but even the raw materials for such creations (film footage, audio samples, etc.), empowering everyone to innovate and do their best work by using the best work of others — all attributable and all fairly compensated. In answer to our question earlier of who gets to decide — we all do, and this is the essence of ABE’s approach. Additionally, ABE achieves this not by navigating the red tape represented by copyright, or by ornamenting it with NFTs as many Web3 initiatives attempt to do, but by cutting the tape in Gordian fashion. ABE is able to fairly compensate people purely on the merits of their contributions that are publicly known and agreed-upon — there is no need for copyright. Indeed, the arbitrariness of copyright is revealed at least in that usually, the copyright holders for creative works aren’t even the creators of the content! ABE makes it possible to rid ourselves of the red tape, greatly increasing the efficiency of the entire system while maximizing fairness to content creators, distributors and consumers alike, to an extent that today is far out of reach.
Jewel is part of a suite of open source projects that are proving this larger concept — that economics is possible, and even better, when we set value free. If you use Jewel and find it to be useful or want to support its goals, and if you decide to contribute financially to it, that money is going to be divided amongst all direct contributors as well as libraries used, and among other projects whose ideas are reflected in Jewel. In other words, if this application provides value to you, the application’s economics are set up in such a way that all contributors to that value you received will be fairly recognized, by means of a process that you yourself can be a part of! This is how things could work in a world where we don’t need to be colleagues in order to sustainably create value together, and is the promise of Attribution Based Economics.
I could say a lot more on the subject, and the incredible nuances of making economics work for everyone while resolving all of the apparent paradoxes such a solution appears to entail. For now, we are focused on prototyping the model in a few pilot projects, and we have a long way to go. Find out more and join us at drym.org. It’s not a startup but a movement. You are a necessary part of the solution rather than a mere spectator to someone else’s grand delusions, and together, we’ll shine as jewels, more brightly than all the shortsighted shards that senselessly seek to steal but a spark of the glory in which we all would partake.